Nuestros excelentísimos señores veteranos quieren organizar una barra legendaria, que pase a la historia como la mejor barra jamás organizada en mates, por lo que han alquilado todo Cocón y han sobornado al portero para que deje colar amigos de otras carreras.
Pero nuestros veteranos no se quedan ahí, para asegurarse de que sea la mejor barra tienen que arreglárselas para que la gente tenga siempre bebida, ni escasa ni en exceso.
Planeando se topan con que: si hay más bebida de la necesaria para la gente de mates (aproximadamente $aleph_0$litros), algunos empezarán a invitar amigos de otras carreras, lo cual reducirá la disponibilidad de bebida y provocará que la gente se aburra y se vaya a otro sitio, regulando de nuevo la cantidad de bebida disponible a los que se quedan.
Esto suena sospechosamente similar a un problema de poblaciones en un ecosistema, 2 grupos que dependen de la población del otro para crecer o extinguirse (bebida y bebedores), lo cual nos da una pista para pensar en el modelo de Lotka-Volterra.
Ecuaciones de Lotka-Volterra
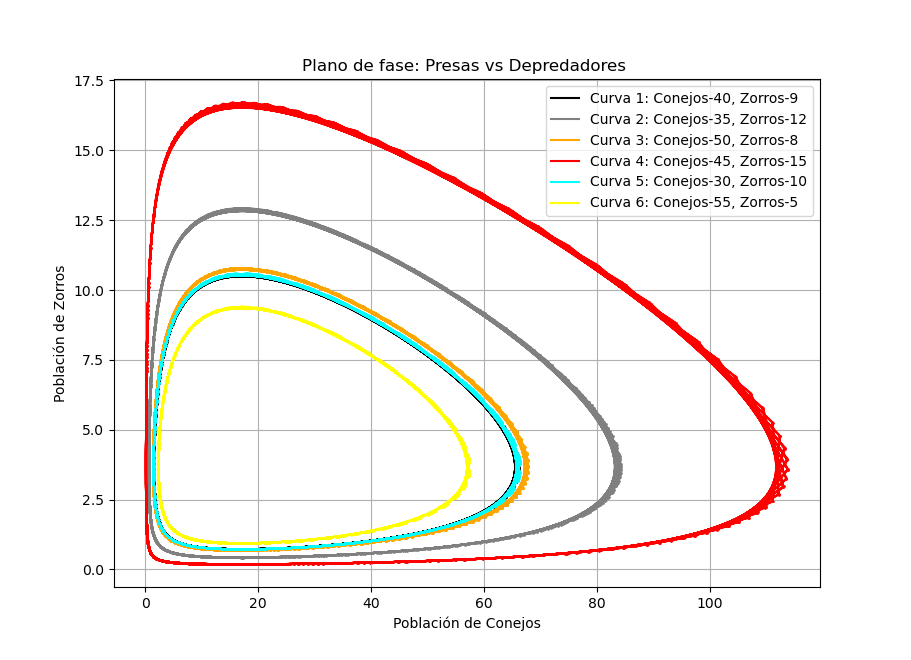
Las ecuaciones de Lotka-Volterra son un sistema de ecuaciones diferenciales que sirven para modelar poblaciones y ecosistemas, por ejemplo nos permiten saber cómo pequeños cambios en una población de conejos va a alterar la futura población de zorros (más conejos implica más comida para los zorros, los zorros se multiplican, los conejos empiezan a escasear, mueren zorros, los conejos se recuperan ...) todo esto ocurre en ciclos regulares como se puede ver en esta gráfica.
Cada color representa un ciclo dado por unas condiciones iniciales, al pasar el tiempo cada anillo se recorre en sentido antihorario, o sea, la población varía de acuerdo a la gráfica en cuestión.
Pero para qué querríamos hacer algo tan trivial e inútil como modelar una poblacion para tomar decisiones, mejorar su estabilidad y bla bla bla, aburrido, vamos a darle un uso serio a estas ecuaciones por el bien de la ciencia, veamos cuánta bebida deberíamos servir en una barra para asegurar la estabilidad de la fiesta.
Considerando las variables:
x = "cantidad de universitarios"
y = "botellas de bebida disponible"
Las ecuaciones de Lotka-Volterra quedarían de la siguiente forma:
$$ \frac{dx}{dt} = \alpha x - \beta x y $$
$$ \frac{dy}{dt} = \delta x y - \gamma y $$
Donde:
α es la tasa de reposición de la bebida.
β representa el consumo de bebida por unidad de tiempo.
ɣ es la tasa de abandono de la barra por escasez de bebida
δ es la tasa de invitaciones en abundancia de bebida.
Bien, una vez presentado el modelo, vamos a dar un "saltito" a su solución, para los curiosos habrá un enlace al final.
Las curvas soluciones tienen la siguiente pinta, en función de las condiciones iniciales (xo,y0)
$$V_{(x_0,y_0)} = \delta x - \gamma ln(x) + \beta y - \alpha ln(y)$$
Estas soluciones se pueden poner en gráficas muy bonitas a mi parecer, como esta:
Entonces ¿Cual es entonces la cantidad de bebida que evita que se acabe la fiesta antes de tiempo?
Vemos que en las curvas más exteriores como la amarilla o naranja el riesgo de acabar por el orígen, o sea, que se acabe la bebida y se vaya todo el mundo, es mayor, por lo que nuestros excelentísimos veteranos deberían acordar un suministro describa una curva más estable, como la roja, la gris o la verde.
Además, estas curvas nos dan información de cuándo el sistema es más frágil para estratégicamente inyectar bebida extra al sistema e impedir que se acabe la fiesta, ese momento se encuentra al llegar al borde izquierdo de la gráfica, así alejaríamos la gráfica del 0 del eje x y pasaríamos a un ciclo más estable.
Enlaces de interés:
(~1 minuto) - Animación cortita
(10 mintos)- Solución de las ecuaciones
(16 minutos ) - Modelo explicado (Numberphile)