
-¡Mi papá es mejor que tu papá!
-No, mi papá es diez veces mejor que el
tuyo.
-¡El mío cien veces más!
-¡El mío mil veces más!
-¡El mío mil veces más!
-¡El mío un millón de veces más!
-¡El mío un billón de veces más!
-¡El mío un gúgol (10^100) de veces más!
Seguro que en
alguna ocasión todos hemos caído en este tipo de violenta batalla numérica,
donde como niños tuvimos ocasión de desplegar todo nuestro arsenal de múltiplos
de diez. Yo personalmente lo más que llegue a decir fue un gúgolplex,
10^(10^100), a lo que inevitablemente seguía la pregunta “¿Eso que diablos
es?”, y tras ella la original aportación “Pues un gúgolplex más uno”. A estas
alturas, era cuando empezaba yo “Un gúgolplex de gúgolplexes de gúgolplexes de
gúgolplexes de ………..”.
Fuera anécdotas, mucha
gente pensará que todos esos números son pura fantasía, y que en matemáticas
“serias” rara vez ves un número de dos cifras (si es que ves números). Pero
esto es radicalmente falso: en una serie de entradas sobre los “grandes números”,
exploraremos números gigantes que aparecen en las matemáticas serias, y que
dejan en ridículo con facilidad al gúgolplex. Y ya que estamos, nos servirá
para engrosar nuestro arsenal numérico para la próxima batalla que pudiera
tener lugar (nota: no recomiendo pelear conmigo en particular jeje).
Empezaremos con
algo simple: contraejemplos. En ocasiones el investigador en matemáticas
envidia a los investigadores de las
ciencias empíricas, y se ve tentado a extrapolar a partir de un patrón. Por
ejemplo, 3 es primo, 31 es primo, 331, como no, es primo. También lo son 3331 y
33331. Y también 333331. Todo matemático leyendo esto seguramente ya esté
pensando: Teorema: ¿Todo número de la forma 3…31 es primo? Hemos comprobado los
primeros casos, y de momento tiene buena pinta… Pues resulta que no, ya que 333333331
es igual a 17*19697843. Teorema arruinado :(
Pero la rama de
teoría de números nos puede traer números mucho mayores que 333333331. Se
define la función contador de números primos π(x) como la cantidad de números
primos entre 0 y x. Un problema
clásico de teoría de números es encontrar una función más fácil de calcular
(pues comprobar todos los primos menores que un número es una tarea difícil) que
aproxime π(x). En particular, existe una función llamada logaritmo
integral de x, li(x), definida como
Y también el logaritmo
integral desplazado, que se define a su vez como
que evita la singularidad para t=1.
Esta segunda
función (aunque la primera también) resulta ser una muy buena aproximación de π(x), y se probó (teorema de los números primos) que
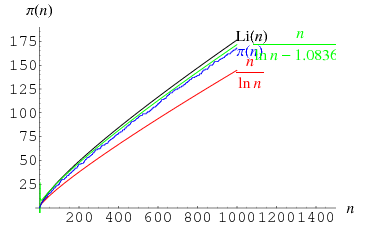
En la imagen se
puede comprobar como varias funciones se aproximan a π(x).
Otra pregunta que
surgió es si li(x) > π(x) para todo x natural, y a la
vista de la ausencia de contraejemplos en los rangos de números que se
comprobaron, muchos matemáticos conjeturaron que la proposición era cierta. Por
poner un ejemplo, para x=1000000000000, π(x)=37607912018 < li(x)=37607950280,80… Con ordenadores actuales,
sabemos que la conjetura se cumple hasta al menos x=1.39*10^17, por lo cual
parecería extraño que no continuara la tendencia.
Pero en 1914,
Littlewood demostró que existía un x
natural tal que π(x) − li(x)
> 0, y es más, que el signo de la expresión cambiaba infinitas veces en el
dominio de los naturales. Luego en 1933 Skewes demostró utilizando la hipótesis de Riemann que tal número debería ser menor que e^(e^(e^79))
< 10^(10^(10^34)). Pero recuerdo al lector que la hipótesis de Riemann (que
afirma que todo los ceros no triviales de la función zeta de Riemann tienen
parte real 1/2), si bien muchos matemáticos conjeturan que es cierta, todavía
no ha sido demostrada, por lo que la cota superior no era del todo
satisfactoria. Más tarde, en 1955, Skewes consiguió hallar, esta vez sin
necesidad de utilizar la hipótesis de Riemann, una cota superior que
aproximadamente es e^(e^(e^(e^7.705))) < 10^(10^(10^964)). Estos dos números
exceden con creces al gúgolplex, pero en la actualidad se han mejorado las
cotas superiores a en torno a e^727,95133, que vemos que es mucho menor que el
gúgolplex.
 También aparecen
números de inmensa magnitud en estructuras algebraicas. Por ejemplo, hace poco
se terminó de probar el teorema de la clasificación de los grupos simples
finitos, que los divide
en 18 familias infinitas numerables y 26 “grupos
esporádicos”, que no son bloques de construcción de las otras familias. Ya es
raro que justamente haya 26 de tales grupos, pero lo sorprendente es su gran
tamaño. El más grande de ellos, el grupo
monstruo, consta de ni nada más ni nada menos
También aparecen
números de inmensa magnitud en estructuras algebraicas. Por ejemplo, hace poco
se terminó de probar el teorema de la clasificación de los grupos simples
finitos, que los divide
en 18 familias infinitas numerables y 26 “grupos
esporádicos”, que no son bloques de construcción de las otras familias. Ya es
raro que justamente haya 26 de tales grupos, pero lo sorprendente es su gran
tamaño. El más grande de ellos, el grupo
monstruo, consta de ni nada más ni nada menos
808017424794512875886459904961710757005754368000000000≈
8×1053
elementos,
que pese a no ser tan grande como la cifra anterior, sigue siendo igualmente
impresionante. Se adjunta como curiosidad la imagen de las relaciones de
contención entre los 26 grupos esporádicos (como se indica en Wikipedia, hay un
pequeño error en ella, debería ir una línea de M11 a ON).
Pero todavía no
hemos hecho nada más que empezar. Estos números
no es que sean excesivamente grandes, sin gran esfuerzo podemos poner ((31415926535!)!)!,
que es mayor que ambos (por si alguien no se lo cree, se puede ver con la
aproximación de Stirling y tomando logaritmos que supera ambos números con
creces). Los números grandes de verdad no se pueden representar con la notación
usual, por mucho que abuses de factoriales y de torres de exponenciales. En la
siguiente entrada de “Grandes números” aprenderemos como representar números
mucho mayores mediante la notación de Knuth, e inmediatamente después veremos
como ni siquiera esta notación puede acercarse a los números de los que hablaremos.




