(223) Grandes números (I)

-¡Mi papá es mejor que tu papá!

-No, mi papá es diez veces mejor que el tuyo.

-¡El mío cien veces más! 
-¡El mío mil veces más!

-¡El mío un millón de veces más!

-¡El mío un billón de veces más!

-¡El mío un gúgol (10^100) de veces más!

Seguro que en alguna ocasión todos hemos caído en este tipo de violenta batalla numérica, donde como niños tuvimos ocasión de desplegar todo nuestro arsenal de múltiplos de diez. Yo personalmente lo más que llegue a decir fue un gúgolplex, 10^(10^100), a lo que inevitablemente seguía la pregunta “¿Eso que diablos es?”, y tras ella la original aportación “Pues un gúgolplex más uno”. A estas alturas, era cuando empezaba yo “Un gúgolplex de gúgolplexes de gúgolplexes de gúgolplexes de ………..”.

Fuera anécdotas, mucha gente pensará que todos esos números son pura fantasía, y que en matemáticas “serias” rara vez ves un número de dos cifras (si es que ves números). Pero esto es radicalmente falso: en una serie de entradas sobre los “grandes números”, exploraremos números gigantes que aparecen en las matemáticas serias, y que dejan en ridículo con facilidad al gúgolplex. Y ya que estamos, nos servirá para engrosar nuestro arsenal numérico para la próxima batalla que pudiera tener lugar (nota: no recomiendo pelear conmigo en particular jeje).

Empezaremos con algo simple: contraejemplos. En ocasiones el investigador en matemáticas envidia  a los investigadores de las ciencias empíricas, y se ve tentado a extrapolar a partir de un patrón. Por ejemplo, 3 es primo, 31 es primo, 331, como no, es primo. También lo son 3331 y 33331. Y también 333331. Todo matemático leyendo esto seguramente ya esté pensando: Teorema: ¿Todo número de la forma 3…31 es primo? Hemos comprobado los primeros casos, y de momento tiene buena pinta… Pues resulta que no, ya que 333333331 es igual a 17*19697843. Teorema arruinado :(

Pero la rama de teoría de números nos puede traer números mucho mayores que 333333331. Se define la función contador de números primos   π(x) como la cantidad de números primos entre 0 y x. Un problema clásico de teoría de números es encontrar una función más fácil de calcular (pues comprobar todos los primos menores que un número es una tarea difícil) que aproxime π(x).  En particular, existe una función llamada logaritmo integral de x, li(x), definida como

Y también el logaritmo integral desplazado, que se define a su vez como

que evita la singularidad para t=1.

Esta segunda función (aunque la primera también) resulta ser una muy buena aproximación de π(x), y se probó (teorema de los números primos) que

 

En la imagen se puede comprobar como varias funciones se aproximan a π(x).

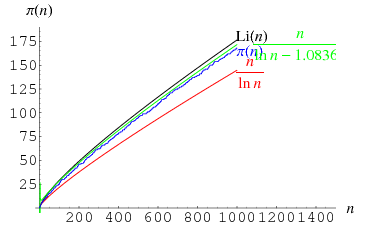
Otra pregunta que surgió es si li(x) > π(x) para todo x natural, y a la vista de la ausencia de contraejemplos en los rangos de números que se comprobaron, muchos matemáticos conjeturaron que la proposición era cierta. Por poner un ejemplo, para x=1000000000000, π(x)=37607912018 < li(x)=37607950280,80… Con ordenadores actuales, sabemos que la conjetura se cumple hasta al menos x=1.39*10^17, por lo cual parecería extraño que no continuara la tendencia.

Pero en 1914, Littlewood demostró que existía un x natural tal que π(x) − li(x) > 0, y es más, que el signo de la expresión cambiaba infinitas veces en el dominio de los naturales. Luego en 1933 Skewes demostró utilizando la hipótesis de Riemann que tal número debería ser menor que e^(e^(e^79)) < 10^(10^(10^34)). Pero recuerdo al lector que la hipótesis de Riemann (que afirma que todo los ceros no triviales de la función zeta de Riemann tienen parte real 1/2), si bien muchos matemáticos conjeturan que es cierta, todavía no ha sido demostrada, por lo que la cota superior no era del todo satisfactoria. Más tarde, en 1955, Skewes consiguió hallar, esta vez sin necesidad de utilizar la hipótesis de Riemann, una cota superior que aproximadamente es e^(e^(e^(e^7.705))) < 10^(10^(10^964)). Estos dos números exceden con creces al gúgolplex, pero en la actualidad se han mejorado las cotas superiores a en torno a e^727,95133, que vemos que es mucho menor que el gúgolplex.

También aparecen números de inmensa magnitud en estructuras algebraicas. Por ejemplo, hace poco se terminó de probar el teorema de la clasificación de los grupos simples finitos, que los divide en 18 familias infinitas numerables  y 26 “grupos esporádicos”, que no son bloques de construcción de las otras familias. Ya es raro que justamente haya 26 de tales grupos, pero lo sorprendente es su gran tamaño.  El más grande de ellos, el grupo monstruo, consta de ni nada más ni nada menos 

 808017424794512875886459904961710757005754368000000000≈ 8×10⁵³ 

elementos, que pese a no ser tan grande como la cifra anterior, sigue siendo igualmente impresionante. Se adjunta como curiosidad la imagen de las relaciones de contención entre los 26 grupos esporádicos (como se indica en Wikipedia, hay un pequeño error en ella, debería ir una línea de M11 a ON).

Pero todavía no hemos hecho nada más que empezar. Estos números  no es que sean excesivamente grandes, sin gran esfuerzo podemos poner ((31415926535!)!)!, que es mayor que ambos (por si alguien no se lo cree, se puede ver con la aproximación de Stirling y tomando logaritmos que supera ambos números con creces). Los números grandes de verdad no se pueden representar con la notación usual, por mucho que abuses de factoriales y de torres de exponenciales. En la siguiente entrada de “Grandes números” aprenderemos como representar números mucho mayores mediante la notación de Knuth, e inmediatamente después veremos como ni siquiera esta notación puede acercarse a los números de los que hablaremos.