( 239 ) El maravilloso mundo de los fractales (I)

Las matemáticas son preciosas (al menos cuando no nos examinamos de ellas). Pero para alguien que no ha dedicado su vida al estudio de estas, es muy difícil discernir algo bello entre la inmensa cantidad de símbolos esotéricos con los que a los matemáticos nos gusta tanto decorar nuestras hojas en sucio. Por lo tanto, si queremos convencer al mundo de la belleza de esta disciplina, debemos ofrecer un resultado más visual que meras fórmulas… ¿Y qué mejor candidato que los famosos fractales?

Comenzaremos con una brevísima introducción histórica: la idea de un objeto que se parezca a una parte del mismo recursivamente ya fue explorada por Leibniz a finales de siglo XVII, pero la idea no fue muy aceptada ni investigada en la época. No fue hasta la llegada de Weierstrass dos siglos después, con su muy patológica función (de la que hablaremos más adelante), cuando el mundo presenció el nacimiento de los fractales. Durante el siglo XX, diversos matemáticos produjeron más ejemplo de fractales, pero la falta de ordenadores y una teoría matemática sólida sobre los fractales dificultaron el florecimiento del campo.

Esto cambió con la llegada de Benoît Mandelbrot. Mandelbrot fue el primer matemático interesado en la naturaleza de los fractales que tuvo acceso a los rudimentarios ordenadores de la época, y con ellos produjo modestas pero muy útiles y novedosas visualizaciones. Fue él además quien acuñó el término fractal en 1975, refiriéndose a “figuras geométricas fracturadas o con bordes intricados que pueden ser divididas en partes, cada una de las cuales es una copia idéntica o aproximada de la original”. Debido a la variedad de objetos que satisfacían estas propiedades, a Mandelbrot le resultó difícil encontrar una definición formal de fractal, hasta que en 1983 escribió:

 “Por definición, un fractal es un subconjunto de un espacio métrico cuya dimensión de Hausdorff es estrictamente mayor que su dimensión topológica (dimensión de Lebesgue).”

Aún con esta definición, Mandelbrot no quedó satisfecho, pues había varios conjuntos autosimilares que no caían en la categoría de fractal. De todos modos, pese a este inconveniente, el trabajo de Mandelbrot resultó fundamental para la solidificación y formalización del campo de los fractales. Este campo no es una simple moda, sino que sigue ganando fuerza en las últimas décadas, presentándose como una valiosa herramienta matemática para comprender ciertos fenómenos del mundo que nos rodea.

Volviendo a la definición anterior, aparecen dos términos que posiblemente resulten desconocidos al lector: la dimensión de Lebesgue y la dimensión de Hausdorff. Si el lector siente curiosidad sobre la definición más formal de estos conceptos, dejaremos un comentario durante los próximos días en esta entrada, que contendrá un enlace a un segundo artículo que las presenta algo más rigurosamente. Dicho artículo, si bien es algo más complicado que lo que solemos tratar en el blog, es sin duda también muy interesante. Si al lector no le apetece leer el artículo extra, bastará con que se crea las siguientes "proposiciones":

-La dimensión de Lebesgue de un conjunto es lo que pensamos intuitivamente: segmento o curva, 1, figura plana o superficie, 2, cuerpo geométrico, 3.

-La dimensión de Hausdorff  es la misma que la de Lebesgue para las conjuntos “normales”, pero es mayor en el caso de los fractales (por definición de fractal).

-Podemos calcular la dimensión de Hausdorff (en realidad calcularemos la de Minkowski, pero no importa, pues lo haremos cuando coincidan) de la siguiente manera: Un fractal es autosimilar, es decir, está formado por copias más pequeñas de sí mismo. Si podemos obtener N copias con una proporción entre el original y cada copia r, entonces la dimensión es D= log(N)/log(r). El lector avispado se habrá dado cuenta de que está fórmula no es exactamente igual a la que aparece en la pizarra detrás de la fotografía de Mandelbrot. Esto es una mera cuestión de notación, en esta entrada consideraremos que r = 2 si podemos extraer de una figuras varias con la mitad de tamaño, mientras que Mandelbrot consideraría en ese mismo caso r = 1/2.

Ahora que ya hemos visto las proposiciones anteriores, podemos comenzar. El modo más fácil e intuitivo de construir fractales es iterando una “operación” geométrica. Comenzaremos con uno de los fractales más simples, el copo de nieve de Koch. Inicialmente se toma un triángulo equilátero, y la operación que se itera es la siguiente: se sustituye el tercio central de cada lado por un triángulo equilátero sin base. Con tres o cuatro iteraciones ya toma una forma característica:

En el copo de Koch, la dimensión de Lebesgue es 1. Veamos cómo calcular la dimensión de Minkowski (que en este caso será igual que la de Hausdorff). Observamos que cada “lado” se transforma en 4 con una longitud igual a 1/3 de la anterior. Al aplicar la fórmula hallada anteriormente nos da que su dimensión es log(4)/log(3) (aprox. 1,2619), que puede ser interpretado como que este conjunto se aproxima más a ser una recta unidimensional que a ser una figura bidimensional.

También se construye con este principio la famosa curva del dragón de Heighway.  Se puede construir partiendo de  un segmento, y en cada iteración recorrer la figura desde un extremo, sustituyendo cada segmento por dos segmentos que formen un ángulo recto, con orientación que siempre comience hacia la derecha y se vaya alternando. Esto hace que se pueda construir muy fácilmente en papel cuadriculado, o plegando una tira de papel (como se observa en la segunda figura). En las imágenes se ve mucho más claro:
 

Su dimensión de Lebesgue es 1, mientras que la de Hausdorff es 2, como bien se aprecia en estas dos figuras. Esto significa que la curva es "densa" sobre el plano, lo cual no resulta del todo sorprendente teniendo en cuenta como se construye y lo que pasa en las regiones interiores (rodeadas por cuatro segmentos de la curva). Sin embargo, la dimensión de su frontera no es tan sencilla: como se menciona en el artículo extra, es aproximadamente 1,52, cosa que simplemente nos vamos a creer, pero el lector es libre de consultar el artículo correspondiente. También cabe remarcar que la curva del dragón encaja consigo misma para “embaldosar el plano”, produciendo estos curiosos patrones.

Ante la cantidad de fractales que se originan siguiendo el sistema expuesto anteriormente, se ha llegado a desarrollar un sistema formal para expresarlos, que resulta de mucha utilidad en campos como la biología, ya que muchas plantas presentan estructuras autosimilares (sin ir más lejos, las ramas de los árboles).

De todos modos, la sustitución no tiene por qué ser de segmentos. Dos de los fractales más característicos, el triángulo y la alfombra de Sierpinski , se construyen sustituyendo polígonos. Como una imagen vale más que mil palabras, su construcción es la que sigue:

Aquí la dimensión de Lebesgue también es 1. Calculemos la dimensión de Minkowski. En el triángulo de Sierpinski para r = 2 es fácil notar que N = 3, por lo que D es log(3)/log(2) (aprox. 1,5850). Tiene sentido,

pues parece que es más “sólido” que el copo de Koch. Por otro lado, para la alfombra de Sierpinski, obtenemos por otra parte una dimensión de log(8)/log(3) (aprox. 1,8927), ya que para r = 3, N = 8. Como curiosidad, estos fractales  tienen primos-hermanos en el espacio tridimensional. Más concretamente, el equivalente de la alfombra de Sierpinski en tres dimensiones se llama esponja de Merger , figura que en el momento de la redacción de esta entrada es la imagen de fondo del blog.

 

Pero no todos los fractales provienen de polígonos regulares… Como contraejemplo, podemos mostrar los tamices de Apolonio, que se basan en inscribir circunferencias tangentes a otras tres sucesivamente (en la imagen se muestra el tamiz con simetría triangular):

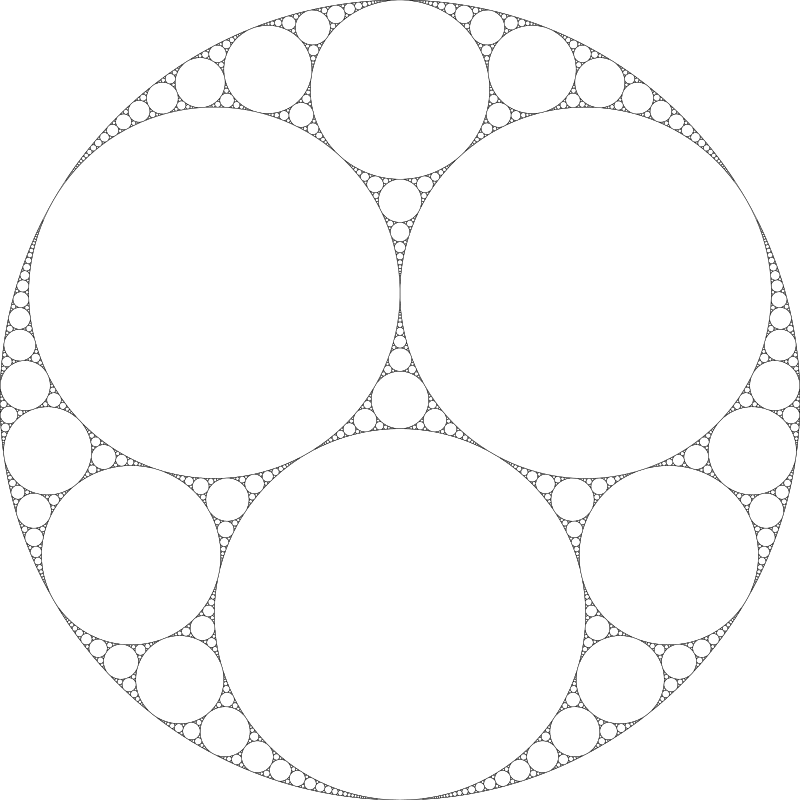
El análisis de la dimensión en este caso es más complicado, así que nos limitaremos a decir que la dimensión de Lebesgue es de nuevo 1, y la de Hausdorff aproximadamente 1,3057.

 Debemos, eso sí, destacar también que los fractales no son simples curiosidades matemáticas en forma de dibujitos. El primer fractal con el que se encuentra un estudiante del grado de Matemáticas es el conjunto de Cantor, conjunto que se obtiene empezando con un intervalo cerrado [0,1] y sustrayendo en cada paso de los intervalos cerrados [a,b] que haya el intervalos abierto (2a/3+b/3,a/3+2b/3), que en el caso del intervalo cerrado inicial, será (1/3,2/3). Este simple procedimiento da lugar a un fractal, pues cada tercio en el que queda dividido es una copia idéntica del conjunto, con un tercio de la longitud, y cada tercio de esos tercios con un noveno de la longitud, y así sucesivamente.

Para el conjunto de Cantor, la dimensión de Lebesgue es 0 y la dimensión de Minkowski  es log(2)/log(3) (aprox. 0,6309), lo cual podría indicar que es “menos” que una línea recta, pero aun así, más que un punto. A estas alturas, al lector no le será difícil deducir cual es el valor exacto como cociente de logaritmos.

Además de ser fractal, este conjunto tiene numerosas propiedades interesantes: pese a que su medida es cero, contiene un número incontable de puntos. Además, por parte de su topología, es un conjunto compacto y denso que no contiene ningún intervalo abierto y es completamente inconexo. En conclusión, los fractales no son una “figura” sin más.

También debemos volver a la función de Weierstrass, que sirvió para mostrar que la continuidad de una función no implicaba la diferenciabilidad en ningún punto (más técnicamente, podemos construir una función continua en un intervalo tal que el conjunto de puntos en los que la función sea diferenciable tenga medida 0). Se define a partir de la siguiente serie de Fourier,

con a y b cumpliendo que 0<a<1, b es un natural positivo, y 

 




Como dijimos antes, esta función presenta un gran interés en análisis como contraejemplo, y además su gráfica es un fractal. En la imagen se aprecia su carácter autosimilar, y su dimensión de Hausdorff está acotada por

 


que se cree que es el valor exacto.  Gaussianos estudia más en detalle la función de Weierstrass en el siguiente artículo.

En resumen, en esta entrada hemos explorado los fractales clásicos, los que se conocían antes del nacimiento de la computación. En la siguiente entrada exploraremos los fractales nuevos, entre ellos el más famoso de todos, el conjunto de Mandelbrot.

( 233 ) Descubierto un nuevo primo de Mersenne

     No es habitual que en la prensa generalista (lo que vienen siendo los diarios de toda la vida) aparezcan noticias relacionadas con las matemáticas. Entendámonos, tampoco es que no salgan nunca. De vez en cuando las matemáticas del bachillerato se hacen notar (por ejemplo, conflictos en la selectividad: el año pasado, o también el año anterior con un problema que se hace especialmente difícil) o se da algún premio a algún matemático (por ejemplo, un premio de este año y también, aunque es ya más antiguo una noticia que ayuda a luchar contra la discriminación de género) o incluso, y esto es el tipo de artículos que no podemos dejar de recoger en este blog, sale de vez en cuando una noticia sobre lo bien que se colocan los matemáticos (eso ya lo hemos tratado anteriormente en otras entradas, como esta) o sobre la importancia que tienen las matemáticas en nuestra sociedad. En esta línea tenemos este artículo de noviembre pasado, "El boom de las matemáticas", del cual nos permitimos reproducir el primer párrafo para animar a su lectura:

Decía el novelista Graham Greene que «una pasión tiene que tener algo de clandestino, algo de transgresor y algo de perverso». En un mundo en el que los números se pueden usar para cosas tan dispares como navegar por internet o explicar el funcionamiento de las estrellas, las matemáticas pueden ser la pasión de muchas personas. Pero no todos los afortunados con este don lo reconocen, quizás porque al ser tan complejas y abstractas como la realidad en sí misma, las matemáticas pueden llegar a ser abrumadoras para los profanos en la materia. Por eso no sorprende que los apasionados por los números a veces queden encajados en la categoría de los raros.

     Pero también alguna vez, y esto es todavía más raro, lo que aparece en la prensa es la noticia de un descubrimiento matemático. Eso es justo lo que ha ocurrido el pasado mes de enero, así que nosotros vamos a recogerlo aquí para intentar explicar un poco la noticia y, quien sabe, quizá ayudar a difundirla un poco (¿es posible que haya estudiantes de matemáticas que no lean periódicos y como consecuencia, no estén al tanto de la evolución de la ciencia objeto de sus estudios?, ¿es incluso probable?..., demasiadas preguntas para responder en este humilde blog). 

Logotipo del GIMPS

     El responsable del descubrimiento es un grupo de trabajo (¿quizá deberíamos llamarlo un proyecto de investigación?) llamado GIMPS (iniciales de Great Internet Mersenne Prime Search, o dicho en castellano Gran Búsqueda de Primos de Mersenne por Internet) y la nota de prensa con la que comunican su hallazgo la emitieron el 7 de enero de 2016. El hallazgo que anunciaban es que habían encontrado el mayor número primo que se conoce, que, como se puede esperar dado el nombre del grupo, es un primo de Mersenne. Naturalmente, no el mayor primo que existe porque ya los antiguos matemáticos griegos habían demostrado que hay infinitos números primos. El mayor que conocemos hasta ahora, que dicho sea de paso, es bastante grande. Y esta frase es sólo una excusa para sacar a colación que hemos dedicado ya una entrada a números grandes y tenemos pendiente alguna más, pero digamos que el primo encontrado tiene más de 22 millones de cifras (22.338 618 para ser exactos). Por poner un ejemplo, en el Quijote que tengo en casa caben unos 62 símbolos por linea (incluyendo espacios) y unas 30 líneas por página, así que escribiendo las cifras del primo hallado seguidas, sin huecos, línea tras línea y página tras página a ese mismo tamaño ocuparían aproximadamente 12000 páginas. Mi Quijote ocupa unas 1550 páginas, así que tenemos un número de casi 8 Quijotes.
       El contenido de la nota de prensa acabó apareciendo en los periódicos clásicos (por ejemplo la noticia sale en el ABC el 21 de enero), en los digitales (aquí ponemos un articulo de El Español del 28 de enero que encontramos especialmente claro y completo) o en los blogs de divulgación matemática (el estupendo blog Gaussianos lo ha tenido como entrada con el título: Confirmado el descubrimiento del primo de Mersenne número 49). El número concreto, el primo de Mersenne más grande que se conoce, que aún no lo hemos dicho, es el que aparece en la foto que colocamos aquí debajo (tranquilos que no estan los 22 millones de cifras):

El nuevo primo descubierto (foto sacada del ABC)

     Básicamente, eso es lo que teníamos que contar, pero ya que estamos metidos en harina, que menos que incluir algunos comentarios aclaratorios sencillos. El primero, ¿qué es un primo de Mersenne?, pues simplemente un número primo que es una unidad menor que una potencia de dos. Es decir un primo de la forma 2^P-1. No es difícil ver que entonces el exponente P también tiene que ser un número primo. Ojo, pero no basta con que P sea primo para que 2^P-1 lo sea. Eso sólo pasa para algunos pocos primos.

Portada de una obra del padre Mersenne

      De hecho la hipótesis del cura que los estudió y les dio nombre, el padre Marin Mersenne, es que a partir de P=257 ya ningún número de esa forma es primo, lo cual no es cierto.  El padre Mersenne fue compañero de colegio de René Descartes y estudió teología, filosofía, teoría musical y, claro está, matemáticas (de hecho fue miembro de la orden de los mínimos, que no tiene nada que ver pero suena a orden para matemáticos). Volviendo a su estudio de primos, no hagamos sangre, se equivocó, pero tampoco hay tantos primos de esa forma especial. Hasta ahora sólo se conocen 49 primos de Mersenne (el número 13 es 2²⁵¹-1, de hecho justo el 2²⁵⁷-1 no es primo, luego hay 36 hasta ahora con los que el padre Marsenne no contaba). Conviene aclarar que los primeros que se conocen son todos los que hay, es decir, que hasta el primo de Marsenne número 44, que es el 2^32.582.657-1 (que se acerca a las diez millones de cifras, exactamente 9.808.358, unos tres Quijotes y medio), todos los numeros de esa forma (una unidad menos que una potencia de dos) y menores que este, distintos de los 44 conocidos, seguro que no son primos. Pero de ahí para arriba es distinto. Se conocen cinco primos más, pero puede que haya algún primo más de esa forma menor que los conocidos. Es decir que el 49 primo de Mersenne, el que se acaba de encontrar, todavía puede acabar siendo el 50 o el 51.
       La ventaja de estos números, de los que son una unidad menos que una potencia de dos, es que hay métodos de cálculo que permiten saber con más rapidez si son primos o no (quiere decir comparado con saber si es primo o no un número de un tamaño parecido pero que no tiene esa forma). De ahí que si uno mira la lista de los primos que fueron en su momento los más grandes conocidos, los 16 últimos encontrados son primos de Mersenne (el último que no lo era se encontró en 1989, entonces era el primo más grande conocido y fue el (391581×2²¹⁶¹⁹³)-1 que tiene 65087 dígitos (tan pequeño que casi ni merece la pena pasarlo a Quijotes, 35 páginas, poco más de tres capítulos). Aclaremos que eso no es lo mismo que los primos más grandes que se conocen ahora (hay primos que no han sido los más grandes conocidos cuando se encontraron, pero al encontrarse en, por decir algo, 2007, eran mayores que el que tuvo el record en 1989). Los 11 primos mayores que se conocen ahora son primos de Marsenne pero el décimo segundo, encontrado en 2007, es el (19249×2^13018586)+1 que tiene casi cuatro millones de cifras (exactamente 3.918.990, este ya pesa algo más de un Quijote).
     Esta característica de los primos de Mersenne hizo que surgiera un proyecto para buscar primos muy grandes de ese tipo, el ya mencionado GIMPS. Como, aún con todas las facilidades ya aprovechadas, la cantidad de cálculos que hay que hacer es muy grande, este proyecto utiliza a través de internet ordenadores que voluntarios le prestan. De ahí que los que figuran como descubridores de los números no son siempre los mismos, aunque todos lo hagan a través del GIMPS, o que puedan aparecer noticias curiosas como este titular de El País de hace 11 años: Un oculista alemán halla el número primo más alto conocido. Se refería al primo de Mersenne número 42 (7.816.230 cifras, algo menos de tres Quijotes de número).
      Sólo nos quedan dos cosas más para terminar esta entrada. La primera, agradecer a Diego Alonso, que nos envió un correo alertándonos del descubrimiento de este primo de Mersenne. Y la segunda, disculparnos con él porque pese a su sugerencia, no tratamos aquí de números perfectos y su relación con primos de Mersenne. No es que el tema no sea interesante, pero prefiero no alargarme más. Tal vez más adelante podría venir otra entrada hablando de números perfectos (y ayudaría si hubiera varios comentarios interesándose en el tema, que no conseguimos temas que os animen a comentar las entradas).