Las matemáticas son preciosas (al menos cuando no nos examinamos de ellas). Pero para alguien que no ha dedicado su vida al estudio de estas, es muy difícil discernir algo bello entre la inmensa cantidad de símbolos esotéricos con los que a los matemáticos nos gusta tanto decorar nuestras hojas en sucio. Por lo tanto, si queremos convencer al mundo de la belleza de esta disciplina, debemos ofrecer un resultado más visual que meras fórmulas… ¿Y qué mejor candidato que los famosos fractales?
Comenzaremos con una brevísima introducción histórica: la idea de un objeto que se parezca a una parte del mismo recursivamente ya fue explorada por Leibniz a finales de siglo XVII, pero la idea no fue muy aceptada ni investigada en la época. No fue hasta la llegada de Weierstrass dos siglos después, con su muy patológica función (de la que hablaremos más adelante), cuando el mundo presenció el nacimiento de los fractales. Durante el siglo XX, diversos matemáticos produjeron más ejemplo de fractales, pero la falta de ordenadores y una teoría matemática sólida sobre los fractales dificultaron el florecimiento del campo.
Esto cambió con la llegada de Benoît Mandelbrot. Mandelbrot fue el primer matemático interesado en la naturaleza de los fractales que tuvo acceso a los rudimentarios ordenadores de la época, y con ellos produjo modestas pero muy útiles y novedosas visualizaciones. Fue él además quien acuñó el término fractal en 1975, refiriéndose a “figuras geométricas fracturadas o con bordes intricados que pueden ser divididas en partes, cada una de las cuales es una copia idéntica o aproximada de la original”. Debido a la variedad de objetos que satisfacían estas propiedades, a Mandelbrot le resultó difícil encontrar una definición formal de fractal, hasta que en 1983 escribió:
“Por definición, un fractal es un subconjunto de un espacio métrico cuya dimensión de Hausdorff es estrictamente mayor que su dimensión topológica (dimensión de Lebesgue).”
Volviendo a la definición anterior, aparecen dos términos que posiblemente resulten desconocidos al lector: la dimensión de Lebesgue y la dimensión de Hausdorff. Si el lector siente curiosidad sobre la definición más formal de estos conceptos, dejaremos un comentario durante los próximos días en esta entrada, que contendrá un enlace a un segundo artículo que las presenta algo más rigurosamente. Dicho artículo, si bien es algo más complicado que lo que solemos tratar en el blog, es sin duda también muy interesante. Si al lector no le apetece leer el artículo extra, bastará con que se crea las siguientes "proposiciones":
-La dimensión de Lebesgue de un conjunto es lo que pensamos intuitivamente: segmento o curva, 1, figura plana o superficie, 2, cuerpo geométrico, 3.
-La dimensión de Hausdorff es la misma que la de Lebesgue para las conjuntos “normales”, pero es mayor en el caso de los fractales (por definición de fractal).
-Podemos calcular la dimensión de Hausdorff (en realidad calcularemos la de Minkowski, pero no importa, pues lo haremos cuando coincidan) de la siguiente manera: Un fractal es autosimilar, es decir, está formado por copias más pequeñas de sí mismo. Si podemos obtener N copias con una proporción entre el original y cada copia r, entonces la dimensión es D= log(N)/log(r). El lector avispado se habrá dado cuenta de que está fórmula no es exactamente igual a la que aparece en la pizarra detrás de la fotografía de Mandelbrot. Esto es una mera cuestión de notación, en esta entrada consideraremos que r = 2 si podemos extraer de una figuras varias con la mitad de tamaño, mientras que Mandelbrot consideraría en ese mismo caso r = 1/2.
Ahora que ya hemos visto las proposiciones anteriores, podemos comenzar. El modo más fácil e intuitivo de construir fractales es iterando una “operación” geométrica. Comenzaremos con uno de los fractales más simples, el copo de nieve de Koch. Inicialmente se toma un triángulo equilátero, y la operación que se itera es la siguiente: se sustituye el tercio central de cada lado por un triángulo equilátero sin base. Con tres o cuatro iteraciones ya toma una forma característica:
En el copo de Koch, la dimensión de Lebesgue es 1. Veamos cómo calcular la dimensión de Minkowski (que en este caso será igual que la de Hausdorff). Observamos que cada “lado” se transforma en 4 con una longitud igual a 1/3 de la anterior. Al aplicar la fórmula hallada anteriormente nos da que su dimensión es log(4)/log(3) (aprox. 1,2619), que puede ser interpretado como que este conjunto se aproxima más a ser una recta unidimensional que a ser una figura bidimensional.
También se construye con este principio la famosa curva del dragón de Heighway. Se puede construir partiendo de un segmento, y en cada iteración recorrer la figura desde un extremo, sustituyendo cada segmento por dos segmentos que formen un ángulo recto, con orientación que siempre comience hacia la derecha y se vaya alternando. Esto hace que se pueda construir muy fácilmente en papel cuadriculado, o plegando una tira de papel (como se observa en la segunda figura). En las imágenes se ve mucho más claro:
Ante la cantidad de fractales que se originan siguiendo el sistema expuesto anteriormente, se ha llegado a desarrollar un sistema formal para expresarlos, que resulta de mucha utilidad en campos como la biología, ya que muchas plantas presentan estructuras autosimilares (sin ir más lejos, las ramas de los árboles).
De todos modos, la sustitución no tiene por qué ser de segmentos. Dos de los fractales más característicos, el triángulo y la alfombra de Sierpinski , se construyen sustituyendo polígonos. Como una imagen vale más que mil palabras, su construcción es la que sigue:
Aquí la dimensión de Lebesgue también es 1. Calculemos la dimensión de Minkowski. En el triángulo de Sierpinski para r = 2 es fácil notar que N = 3, por lo que D es log(3)/log(2) (aprox. 1,5850). Tiene sentido,
pues parece que es más “sólido” que el copo de Koch. Por otro lado, para la alfombra de Sierpinski, obtenemos por otra parte una dimensión de log(8)/log(3) (aprox. 1,8927), ya que para r = 3, N = 8. Como curiosidad, estos fractales tienen primos-hermanos en el espacio tridimensional. Más concretamente, el equivalente de la alfombra de Sierpinski en tres dimensiones se llama esponja de Merger , figura que en el momento de la redacción de esta entrada es la imagen de fondo del blog.
pues parece que es más “sólido” que el copo de Koch. Por otro lado, para la alfombra de Sierpinski, obtenemos por otra parte una dimensión de log(8)/log(3) (aprox. 1,8927), ya que para r = 3, N = 8. Como curiosidad, estos fractales tienen primos-hermanos en el espacio tridimensional. Más concretamente, el equivalente de la alfombra de Sierpinski en tres dimensiones se llama esponja de Merger , figura que en el momento de la redacción de esta entrada es la imagen de fondo del blog.
Pero no todos los fractales provienen de polígonos regulares… Como contraejemplo, podemos mostrar los tamices de Apolonio, que se basan en inscribir circunferencias tangentes a otras tres sucesivamente (en la imagen se muestra el tamiz con simetría triangular):
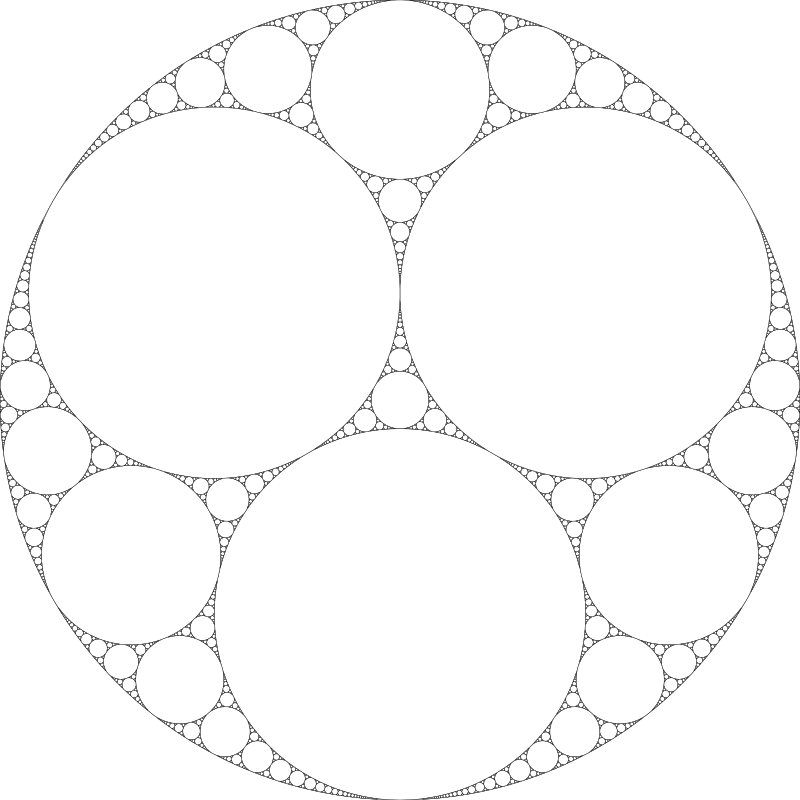
El análisis de la dimensión en este caso es más complicado, así que nos limitaremos a decir que la dimensión de Lebesgue es de nuevo 1, y la de Hausdorff aproximadamente 1,3057.
Debemos, eso sí, destacar también que los fractales no son simples curiosidades matemáticas en forma de dibujitos. El primer fractal con el que se encuentra un estudiante del grado de Matemáticas es el conjunto de Cantor, conjunto que se obtiene empezando con un intervalo cerrado [0,1] y sustrayendo en cada paso de los intervalos cerrados [a,b] que haya el intervalos abierto (2a/3+b/3,a/3+2b/3), que en el caso del intervalo cerrado inicial, será (1/3,2/3). Este simple procedimiento da lugar a un fractal, pues cada tercio en el que queda dividido es una copia idéntica del conjunto, con un tercio de la longitud, y cada tercio de esos tercios con un noveno de la longitud, y así sucesivamente.
Para el conjunto de Cantor, la dimensión de Lebesgue es 0 y la dimensión de Minkowski es log(2)/log(3) (aprox. 0,6309), lo cual podría indicar que es “menos” que una línea recta, pero aun así, más que un punto. A estas alturas, al lector no le será difícil deducir cual es el valor exacto como cociente de logaritmos.
Además de ser fractal, este conjunto tiene numerosas propiedades interesantes: pese a que su medida es cero, contiene un número incontable de puntos. Además, por parte de su topología, es un conjunto compacto y denso que no contiene ningún intervalo abierto y es completamente inconexo. En conclusión, los fractales no son una “figura” sin más.
También debemos volver a la función de Weierstrass, que sirvió para mostrar que la continuidad de una función no implicaba la diferenciabilidad en ningún punto (más técnicamente, podemos construir una función continua en un intervalo tal que el conjunto de puntos en los que la función sea diferenciable tenga medida 0). Se define a partir de la siguiente serie de Fourier,
con a y b cumpliendo que 0<a<1, b es un natural positivo, y
Como dijimos antes, esta función presenta un gran interés en análisis como contraejemplo, y además su gráfica es un fractal. En la imagen se aprecia su carácter autosimilar, y su dimensión de Hausdorff está acotada por
que se cree que es el valor exacto. Gaussianos estudia más en detalle la función de Weierstrass en el siguiente artículo.
En resumen, en esta entrada hemos explorado los fractales clásicos, los que se conocían antes del nacimiento de la computación. En la siguiente entrada exploraremos los fractales nuevos, entre ellos el más famoso de todos, el conjunto de Mandelbrot.
No hay comentarios:
Publicar un comentario