Consideremos un triángulo cualquiera de vértices A, B, C. Dibujemos el punto medio de cada pareja de vértices A’, B’, C’. Unamos cada vértice con el punto medio del lado opuesto. A este segmento de recta se lo conoce como mediana.
Volvamos ahora a nuestro triángulo original, y dibujemos en cada vértice la bisectriz, es decir, la recta que subdivide el ángulo en dos subángulos iguales.
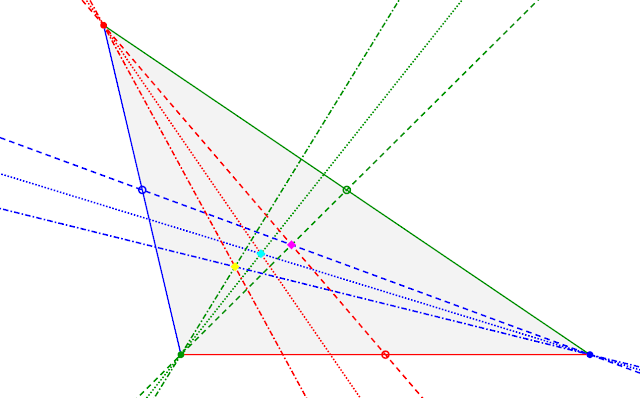
Ahora tenemos dos segmentos que pasan por cada vértice. En cada uno de los vértices, reflejemos cada mediana por su bisectriz, es decir, trazar la imagen especular de la mediana la situar un espejo en la bisectriz. Este segmento de recta se le conoce como simediana (en inglés symmedian de symmetric median – mediana simétrica por su construcción). La simediana tiene una importante propiedad: forma con su bisectriz el mismo ángulo que la bisectriz forma con la mediana, dicho de otro modo, la bisectriz del par mediana-simediana es la misma que la del vértice en el que parten.
Sabemos que las bisectrices se cortan en un punto llamado incentro (centro de la circunferencia circunscrita al triángulo - X(1) en la enciclopedia de centros de triángulos), y las medianas en el centroide (el centro de masa al colocar masas idénticas en los vértices - X(4) en la enciclopedia de centros de triángulos). Las tres simedianas de un triángulo también se cortan en un punto: el punto de Lemoine-Grebe o el punto simediano (el X(6) en la enciclopedia de centros de triángulos).
Esta construcción que en principio parece tan arbitraria tiene su por qué: Tanto la mediana, la bisectriz, o la simediana son cevianas, ternas de rectas o de segmentos de rectas que pasan por los vértices de un triángulo y algún punto del lado opuesto. A los pares de rectas reflejados respecto a la bisectriz se los llama conjugados isogonales (nótese que la bisectriz es su conjugada reflejada isogonal). Además, esta propiedad además de ser la mediana una ceviana hace que la simediana herede propiedades muy buenas y deseables. Por ejemplo, un teorema nos dice que si tres cevianas se cortan en un punto, sendas tres conjugadas isogonales también se cortan en un punto.
Volvamos ahora a nuestro triángulo original, y dibujemos en cada vértice la bisectriz, es decir, la recta que subdivide el ángulo en dos subángulos iguales.
Ahora tenemos dos segmentos que pasan por cada vértice. En cada uno de los vértices, reflejemos cada mediana por su bisectriz, es decir, trazar la imagen especular de la mediana la situar un espejo en la bisectriz. Este segmento de recta se le conoce como simediana (en inglés symmedian de symmetric median – mediana simétrica por su construcción). La simediana tiene una importante propiedad: forma con su bisectriz el mismo ángulo que la bisectriz forma con la mediana, dicho de otro modo, la bisectriz del par mediana-simediana es la misma que la del vértice en el que parten.
Sabemos que las bisectrices se cortan en un punto llamado incentro (centro de la circunferencia circunscrita al triángulo - X(1) en la enciclopedia de centros de triángulos), y las medianas en el centroide (el centro de masa al colocar masas idénticas en los vértices - X(4) en la enciclopedia de centros de triángulos). Las tres simedianas de un triángulo también se cortan en un punto: el punto de Lemoine-Grebe o el punto simediano (el X(6) en la enciclopedia de centros de triángulos).
Esta construcción que en principio parece tan arbitraria tiene su por qué: Tanto la mediana, la bisectriz, o la simediana son cevianas, ternas de rectas o de segmentos de rectas que pasan por los vértices de un triángulo y algún punto del lado opuesto. A los pares de rectas reflejados respecto a la bisectriz se los llama conjugados isogonales (nótese que la bisectriz es su conjugada reflejada isogonal). Además, esta propiedad además de ser la mediana una ceviana hace que la simediana herede propiedades muy buenas y deseables. Por ejemplo, un teorema nos dice que si tres cevianas se cortan en un punto, sendas tres conjugadas isogonales también se cortan en un punto.
 |
| Las rectas a rayas son las medianas, las punteadas son las bisectrices, y las rayadas-punteadas son las simedianas. En magenta el centroide, en cian el incentro, y en amarillo el punto de Lemoine-Grebe. |
Autor: Đɑvɪẟ Ƒernández-De la Cruʒ.
No hay comentarios:
Publicar un comentario