Se aproxima el segundo cuatrimestre, y con él, un nuevo
periodo de matriculación. Es habitual encontrarte con alumnos de tercero y
cuarto indecisos frente a las posibles asignaturas optativas que tenemos en
último curso. Surgen muchas preguntas: ¿Dé que va esa asignatura? ¿Qué
conocimientos previos necesito para aquella otra? ¿Requerirá mucho tiempo esta
otra? Y… seamos honestos, ¿Será fácil de aprobar? Intentaremos responder de la
forma más “objetiva” a todas estas cuestiones, considerando las valoraciones
que nos han transmitido los propios profesores que van a impartirlas.
En este segundo periodo académico podemos elegir entre “seis”
(pues los horarios se
solapan en algunos casos) asignaturas, todas ellas de 6 ECTS:
PROCESOS
ESTOCÁSTICOS
Profesor responsable: Tasio del Barrio
Departamento: Estadística e Investigación Operativa
Conocimientos previos: Es necesario manejar conocimientos básicos de cálculo de
probabilidades, álgebra matricial y ecuaciones diferenciales. Guía Docente
Valoración / Motivaciones / Dificultad:
Los procesos estocásticos
son modelos matemáticos para fenómenos aleatorios que evolucionan en el tiempo.
Las aplicaciones de tales modelos son variadas, incluyendo, por ejemplo, la
valoración de derivados financieros, el diseño de protocolos de transmisión de
datos o de algoritmos de ranking como el PageRank de Google. Al mismo tiempo
los procesos estocásticos son un campo de investigación activa en Matemáticas,
con presencia destacada en las tres últimas ediciones de las medallas Fields
(entre otros, la medalla fue concedida a W. Werner, S. Smirnov y M. Hairer por
sus contribuciones relacionadas con distintos aspectos de los procesos
estocásticos).
 |
| Andréi Márkov |
En esta
asignatura se introducen los modelos más simples de procesos (esto permite que
se pueda cursar la materia sin demasiados requisitos previos), en especial
modelos de Markov (modelos con "memoria corta") y procesos de Poisson.
Se estudia la estructura de tales procesos y su comportamiento a largo plazo.
Con los procesos de Poisson se introduce un cierto "cálculo estocástico"
(cálculo diferencial e integral con respecto a procesos). Este cálculo
estocástico está en la base de los modelos de matemática financiera en las que
se basa la valoración de derivados (aunque la teoría que se presenta en este
curso no alcanza a cubrir este tipo de problemas).
GEOMETRÍA
DIFERENCIAL
Profesor responsable: Javier Finat
Departamento: Álgebra, Análisis Matemático, Geometría y Topología
Conocimientos previos: Son fundamentales las asignaturas de “Topología”, “Análisis
Matemático”, “Álgebra y Geometría Lineales II” y “Geometría de Curvas y
Superficies”. También es recomendable tener presentes los conocimientos de “Ecuaciones
Diferenciales” y “Ampliación de Análisis Matemático”. Guía Docente
Valoración / Motivaciones / Dificultad:
La Geometría
Diferencial trata de caracterizar variedades a partir de propiedades
invariantes por “deformaciones”. Una variedad se obtiene “pegando” datos
locales que son equivalentes a espacios cartesianos. Para ello, utiliza transformaciones suaves de
coordenadas y estructuras superpuestas
que permiten linealizar el estudio de las propiedades o bien identificar las
simetrías locales en los objetos. Por ello, es una extensión natural de
Geometrías Lineales Clásicas bien conocidas.
Un ejemplo
típico es la representación cartográfica de la Tierra en términos de cartas
geográficas que se agrupan en atlas. Incluso para objetos tan simples como la
esfera 2D, existe un gran número de diferentes representaciones cartográficas,
aunque todas ellas son compatibles con la estructura global de la esfera. Este
enfoque se aplica a cualquier otro objeto volumétrico del mundo real acotado
por una superficie y, con más generalidad, a objetos ideales más generales con
una estructura “suave a trozos”, incluyendo la posibilidad de deformaciones
suaves a trozos.
Las
relaciones entre variedades se expresan de forma más sencilla linealizando el
problema en términos de estructuras superpuestas. Las estructuras iniciales que
se superponen a variedades son fibrados tangentes, cotangentes (duales de los
tangentes), principales u otros tensoriales más generales. Para construir
objetos globales sobre estas estructuras superpuestas se utilizan las
mismas herramientas de “pegado” para los
datos locales. La transferencia entre propiedades locales y globales es un
tópico importante, así como la identificación de las propiedades extrínsecas o
intrínsecas de los objetos, es decir, dependientes o no de la inmersión en un
espacio con propiedades más fáciles de identificar. Para ello, se utilizan
campos, formas y sus productos.
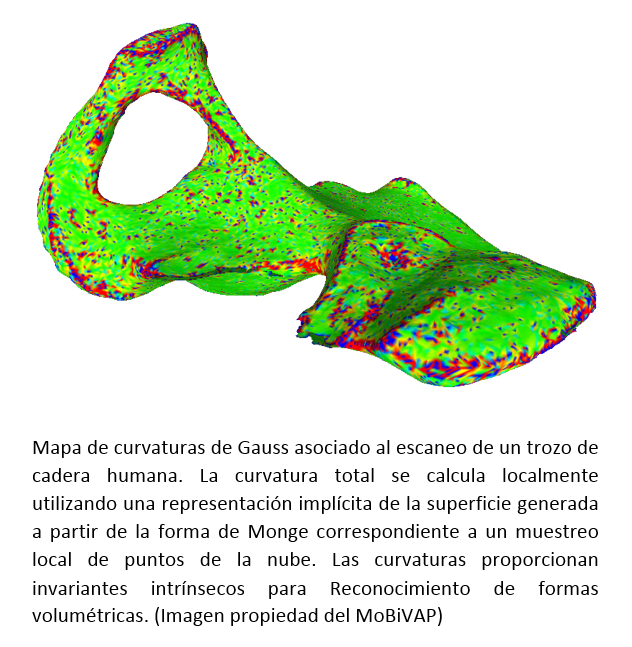 La
aproximación al estudio de objetos basada en Geometría Diferencial proporciona
un soporte para multitud de aplicaciones relacionadas con Física Teórica
(Teorías de Unificación para los diferentes tipos de interacción), Mecánica de
objetos rígidos (movimientos y acoplamientos entre mecanismos, robótica), Mecánica
de Fluidos (elasticidad, viscosidad), Teoría Económica (Micro, Macro, Comercio
Internacional, p.e.), Análisis de Formas y su evolución (en Biología, Geología
o Medicina, p.e.) o, más recientemente, Visión por Computador (análisis de
movimiento, reconocimiento de la forma, representaciones de la interacción,
producción de contenidos 3D para cine o videojuegos, etc).
La
aproximación al estudio de objetos basada en Geometría Diferencial proporciona
un soporte para multitud de aplicaciones relacionadas con Física Teórica
(Teorías de Unificación para los diferentes tipos de interacción), Mecánica de
objetos rígidos (movimientos y acoplamientos entre mecanismos, robótica), Mecánica
de Fluidos (elasticidad, viscosidad), Teoría Económica (Micro, Macro, Comercio
Internacional, p.e.), Análisis de Formas y su evolución (en Biología, Geología
o Medicina, p.e.) o, más recientemente, Visión por Computador (análisis de
movimiento, reconocimiento de la forma, representaciones de la interacción,
producción de contenidos 3D para cine o videojuegos, etc).
Algunas
aplicaciones se muestran en http://www.mobivap.eu/
MÉTODOS
VARIACIONALES EN MATEMÁTICA APLICADA
Profesora responsable: Begoña Cano Urdiales
Departamento: Matemática Aplicada
Conocimientos previos: Se recomienda haber cursado “Ecuaciones Diferenciales” y “Matemática
Aplicada a las Ciencias Sociales y Naturales”. Es aconsejable también la
asignatura de “Ampliación de Ecuaciones Diferenciales” de tercero. Guía Docente
Valoración / Motivaciones / Dificultad:
Se
trata de una asignatura en la que se abordan técnicas para encontrar funciones
que de alguna manera minimicen ciertos funcionales (o funciones de funciones)
bajo algunas restricciones en algunos casos. Para encontrar dichos mínimos se
hará uso de las ecuaciones diferenciales y para plantear el problema matemáticamente
a partir del problema práctico, vendrá bien la experiencia adquirida en la
asignatura "Matemática Aplicada a las Ciencias Naturales y Sociales".
 |
| Catenaria Natural |
En
particular, se estudiará y explicará la forma que debe tener un tobogán si
queremos ir de un punto a otro en el menor tiempo posible, cómo se propaga la
luz en un medio no homogéneo, la forma que adquiere una cuerda de cierta
longitud colgada de dos puntos, la superficie que dibujan las pompas de jabón
una vez determinados los extremos de la misma,...También se estudiarán
cuestiones tales como controlar el nivel de glucosa de un paciente inyectándole
la misma de la forma más conveniente posible o controlar poblaciones de
insectos minimizando la cantidad de insecticidas y la interacción de los
insectos con ciertos alimentos que se podrían contaminar.
Se
pretende que sea una asignatura práctica, interesante y no excesivamente
difícil para los alumnos.
FUNCIONES
GENERALIZADAS Y SUS APLICACIONES
Profesor responsable: Luis Alberto Tristán Vega
Departamento: Álgebra, Análisis Matemático, Geometría y Topología
Conocimientos previos: Los requisitos previos de la asignatura están todos contenidos en asignaturas obligatorias: todas las de Análisis Matemático (funciones de variables reales y de variable compleja, espacios de Banach y espacios de Hilbert), Álgebra Lineal, Topología y Ecuaciones Diferenciales. Guía Docente
Valoración / Motivaciones / Dificultad:
Concretando
más, en el estudio moderno de las EDP es de extremada importancia el
tratamiento "débil" de las ecuaciones, concepto introducido por
Sobolev y que resultó ser equivalente a la teoría desarrollada por Schwartz,
casi simultáneamente, en la primera mitad del siglo XX. De forma muy concisa,
se puede decir que la formulación débil consiste en rebajar las expectativas de
regularidad en las funciones incógnitas, dejando el peso de la derivabilidad a
otras funciones de contraste o de prueba, las denominadas funciones
"test", o rebajando el grado de derivación de la incógnita mediante
procedimientos como la integración por partes. Así, las “soluciones débiles” se
buscan en un conjunto de “distribuciones”, en el terminología de Schwartz, o
“funciones generalizadas”, según la nomenclatura de Sobolev.
En esta
asignatura prestaremos atención a las dos aspectos mencionados; en particular,
veremos que es posible crear un marco adecuado donde se puede, con todo el
rigor y las garantías de una teoría consistente, hablar de la delta de Dirac,
derivarla, calcular sus transformadas de Fourier o de Laplace, etc. La segunda
parte de la asignatura consiste en el estudio de los espacios de Sobolev que
trataremos sólo en dimensión uno debido al tiempo limitado de que disponemos.
Como aplicación obtendremos los resultados principales sobre los problemas
elípticos de contorno (teoría de Sturm-Liouville, etc.) en el caso general, con
coeficientes no constantes, ni siquiera continuos.
*
Contexto de la asignatura:
Esta es
la tercera y última asignatura parte de la materia "Análisis
Funcional" del plan de estudios. Se ha diseñado para que pueda ser cursada
independientemente de “Análisis Real”, la optativa de primer cuatrimestre, pero
evidentemente no tiene sentido cursarla si no se ha cursado primero la
asignatura obligatoria “Introducción a los espacios de funciones”.
En
general, el objetivo del Análisis Funcional es el estudio teórico y analítico
de las ecuaciones funcionales, fundamentalmente en lo que se refiere a
existencia y unicidad de soluciones, y sin él es imposible estudiar Ecuaciones
en Derivadas Parciales (EDP), Cálculo de Variaciones, o Física Matemática, tanto la clásica como la
cuántica (estudiar no es lo mismo que tener noticia de).
*
Descripción de la asignatura:
 |
| Laurent Schwartz |
 |
| Sergei Sobolev |
*
Método docente:
La
actividad docente, tal como se fija en la guía de la asignatura, se articula
mediante la lección magistral, pero esto es una parte mínima del proceso de
aprendizaje. A modo orientativo, el alumno debe dedicar una hora y media de
trabajo individual por cada hora lectiva. El carácter terminal de la asignatura
permite relajar el temario si los plazos temporales así lo exigiesen, y el
ritmo se acomodará al bienestar de alumnos y profesor, y a la óptima
distribución del tiempo de trabajo, no al cumplimiento estricto de un programa;
no se trata de adquirir muchos conocimientos sobre fórmulas o algoritmos, sino
de aprender técnicas de Análisis Matemático avanzado.
Obviamente,
en una materia como esta no caben prácticas informáticas, ni recursos
multimedia; es un paradigma de la abstracción matemática, con el aliciente de
la belleza que supone comprender un gran teorema y el reto de abordar la
complejidad de sofisticadas construcciones teóricas y razonamientos.
*
Conclusión:
La
asignatura es fundamental para aquéllos que deseen comprender muchas de las
aplicaciones de las Matemáticas al estudio de la Naturaleza, proporcionando una
estructura útil para innumerables aplicaciones, pero no se estudiarán ejemplos
concretos mediante procedimientos ad hoc cuya utilidad se limite a un solo
caso.
Por
todo lo mencionado, esta asignatura es muy recomendable para quien pretenda
proseguir su formación académica; será bastante útil, por su valor formativo en
el pensamiento matemático, para quien haya completado todos los créditos
obligatorios; pero no es adecuada para quien sólo desee cumplir con la cuota de
créditos o pretenda obtener unos conocimientos de aplicación cotidiana
inmediata.
CURVAS ALGEBRAICAS
Profesor responsable: Fernando Sanz
Departamento: Álgebra, Análisis Matemático, Geometría y Topología
Conocimientos previos: Es necesario haber adquirido conocimientos básicos de las asignaturas “Estructuras
algebraicas”, “Álgebra Lineal II (Geometría Proyectiva)”, “Topología”, “Análisis
Matemático” y “Geometría Diferencial de Curvas y Superficies”. Guía Docente
Valoración / Motivaciones / Dificultad:
Es una
asignatura optativa del último curso del Grado de Matemáticas. Sirve de
introducción a la rama de las matemáticas conocida como “Geometría Algebraica”.
Esta disciplina, al menos en su motivación inicial, estudia los objetos que
están dados por ecuaciones polinómicas y aprovecha todos los conocimientos del
álgebra (anillos,
cuerpos,
etc.) para estudiar la geometría de tales objetos. A lo mejor te habías
preguntado lo siguiente: en la asignatura “Álgebra y Geometría Lineal” se
estudian los espacios afines (objetos definidos por polinomios de grado uno) y
las cuádricas, especialmente cónicas (objetos definidos por polinomios de grado
dos), pero ¿qué pasa con los objetos definidos por polinomios de grado tres o
más? Son bastante más difíciles que los anteriores porque ya no tienen una ‘estructura
lineal’; éstos son los objetos iniciales de la Geometría Algebraica.
En esta
asignatura, uno se ciñe a las curvas algebraicas planas, objetos definidos en
el plano por un polinomio en dos variables (y su extensión al plano
proyectivo). Muchas de estas curvas las has visto parametrizadas en la
asignatura “Geometría Diferencial” (astroide, cardioide, cúspide, etc) y son
muy utilizadas en óptica, mecánica, teoría de catástrofes, etc. Aquí se ven
atendiendo a su ecuación implícita, que es polinómica. De este modo, podemos
cambiar el cuerpo real por otro cuerpo cualquiera y tenemos objetos distintos
definidos por las mismas ecuaciones y que sirven para diversas aplicaciones:
con cuerpos finitos para la criptografía, con el cuerpo real para visión artificial,
con el cuerpo complejo para sistemas dinámicos, fractales y física teórica,...
Si
pensabas que los conceptos abstractos que has aprendido sobre el álgebra no los
usarías nunca, aquí tienes esta asignatura para desmentirlo. De hecho, casi
todas las disciplinas en matemáticas están interconectadas entre sí y esta
asignatura es un buen ejemplo de ello, donde se usa álgebra, geometría,
análisis y topología (para las curvas complejas).
 |
| Alumnos 2013-2014 |
La
dinámica de las clases es bastante atractiva. Los alumnos van desarrollando la
mayor parte de las lecciones por turnos en la pizarra, siguiendo los textos de
la bibliografía indicados por el profesor. Así el alumno va descubriendo por sí
mismo el mundo de las curvas algebraicas y se enfrenta al proceso matemático de
entender un texto ajeno de matemáticas y explicarlo a compañeros de manera que éstos
también o entiendan.
CÓDIGOS CORRECTORES
Profesor responsable: Félix Delgado de la Mata
Departamento: Álgebra, Análisis Matemático, Geometría y Topología
Conocimientos previos: Es necesario haber adquirido conocimientos básicos de las
asignaturas “Estructuras algebraicas”, “Ecuaciones Algebraicas” e “Informática”. Guía Docente
Valoración / Motivaciones / Dificultad:
Es una asignatura terminal de carrera, en ella se aplicarán
varios de los conocimientos obtenidos en los cursos anteriores (cuerpos
finitos, ecuaciones polinómicas y programación). Se verá la importancia que
tiene en la vida cotidiana la utilización de códigos correctores (comunicación,
transmisión de datos, almacenamiento en memorias, CD's, DVD's...).
El temario introduce diferentes tipos de códigos, sobre todo
correctores, aunque también algunos compresores.
Parte de métodos clásicos de las matemáticas, sobre todo en
el contexto de los cuerpos finitos, explicando su uso en las tecnologías
actuales, sobre todo en el contexto de la comunicación. El uso de los Códigos
Correctores es hoy día bastante estable, separándose en este aspecto de otras
materias semejantes como la criptografía.
En la asignatura también se resolverán algunos interrogantes
del tipo ¿Cómo funciona un CD o DVD? o ¿Pensabas que los cuerpos finitos no
servían para nada?
A nivel general, no es una asignatura que pueda
caracterizarse por una dificultad alta, pues consiste en la aplicación de
conocimientos adquiridos previamente. Después de (al menos) tres años en la
carrera, resulta atractivo encontrarse una asignatura que te muestre la
aplicación práctica de lo que hemos ido aprendiendo.
¡Esperamos que os sea de ayuda para terminar de configurar
vuestro expediente académico!
Como siempre, cualquier duda o sugerencia, podéis comentar en
las entradas del blog, o contactar con nosotros en el correo electrónico:
blogmatematicas.uva@gmail.com
Agradecimiento especial a tod@s los profesor@s que
impartirán estas asignaturas por atendernos y dedicarnos unos minutos para
poder elaborar esta entrada.











